Посадка космического корабля с помощью шейдеров

Введение

Входные условия:

• Имеются два объекта сложной формы, один из которых известен заранее и может быть упрощен для выполнения расчетов
• Алгоритм должен работать в режиме реального времени, без видимой задержки для пользователя

Мы решали эту задачу для применения в медицинской отрасли. Но тот же алгоритм может использоваться и во многих других областях.

В этой статье мы рассмотрим работу алгоритма на примере посадки космического корабля на астероид.

Изображение 1 – Масштаб космического корабля и астероида

Рассмотрим поближе посадочную часть корабля – она состоит из овальной части и четырех стержней-буров, которые используются для закрепления корабля на астероиде.
Задача космонавта – настроить положение космического корабля таким образом, чтобы все стержни находились внутри астероида, а овальная часть плотно прилегала к его поверхности.

Изображение 2 – Вид космического корабля сбоку

Изображение 3 – Вид космического корабля снизу

Очевидное решение

Рассматриваемые объекты – корабль и астероид – являются 3D объектами. Их поверхности представляют собой набор геометрических фигур, как правило, треугольников.
Самое простое решение этой задачи, но не самое эффективное – это пройтись по всем треугольникам объекта и проверить пересечение со вторым объектом с помощью математических формул. Сложность этого алгоритма O(n * m), где n – количество вершин первого объекта, m – количество вершин второго объекта.

Так как вычисления происходят на CPU, они занимают довольно много времени если используется объект с большим количеством вершин. Например, в нашем проекте самый простой объект имел 2744 вершины, самый сложный 17617. Этот способ использует много ресурсов и серьезно нагружает центральный процессор, что приводит к зависанию программы на некоторое время. Очевидно, что это не лучший вариант в нашем случае, когда мы должны пересчитывать карту посадки в реальном времени. Кроме того, перед нами стоит задача визуализации поверхности посадки – вывод результата, понятного для конечного пользователя. После вычисления значений на CPU, нам необходимо будет нарисовать полученный результат каким-либо образом.

Решение посложнее

Для оптимизации вычислений придется пойти более сложным путём и делегировать эти вычисления GPU, используя шейдеры. Если говорить простыми словами, шейдер – это программа, которая выполняется на GPU и позволяет работать с трансформациями объекта, его цветом и освещением. Шейдер отвечает за то, как будет выглядеть объект на экране. Преимущество выполнения вычислений на GPU – это то, что все вершины и пиксели обрабатываются параллельно множеством простых процессоров.

Обычно для выполнения вычислений на GPU используются вычислительные шейдеры.
Однако они поддерживаются не на всех платформах, поэтому, к сожалению, нам не подошли.

Вместо этого мы использовали вертексные и фрагментные шейдеры. Обычно они нужны для трансформации объекта и определения цвета пикселя в цветовой модели RGBA. Фрагментные шейдеры возвращают четырехкомпонентый вектор для каждого пикселя, где каждый компонент определяет значение цвета для R, G, B и прозрачности для A.

Стоит обратить внимание на то, что код шейдера должен быть изолирован и написан применительно только к одному пикселю или вершине. За счет этого он может выполняться параллельно, что в свою очередь значительно увеличивает скорость вычислений.

В алгоритме вертексный шейдер используется для определения глубины объекта – расстояния от камеры до объекта и некоторых вспомогательных свойств. Ниже приведён пример вертексного шейдера. Это метод, который принимает и обрабатывает каждую вершину объекта.

v2f vert(VertIn vertIn) {
    return TransformVertexPosition(vertIn);
}

Затем значения передаются во фрагментный шейдер для выполнения последующих вычислений. В результате фрагментный шейдер возвращает вектор для каждого пикселя, в котором вместо цвета записан результат вычислений. В качестве примера рассмотрим простейший фрагментный шейдер, который записывает расстояние от камеры до объекта в первый компонент вектора.

float frag(v2f i) : COLOR {
    float objectDepth = FormatDepthDependsOnPlatform(i.Z.z);
    return float4(objectDepth, 0, 0, 0);
}

Это метод, который принимает каждую обработанную вершину от вертексного шейдера и вычисляет для нее цвет в конкретном пикселе на картинке. Так как в один и тот же пиксель могут попасть несколько вершин, то результаты выполнения данного метода смешиваются определенным образом. Для этого используется Blending – встроенная возможность шейдера.

Итак, разделим нашу задачу на две подзадачи:

1. Выяснить, насколько примыкает нижняя часть корабля к поверхности астероида
2. Выяснить, находятся ли все стержни внутри астероида

Пересечение основной стыковочной части и астероида

Начнем с первого пункта. Так как нам важна лишь внешняя часть стыковочного механизма, мы можем упростить модель и отрезать лишнее. Оставим только крайние бэкфейсы – задние грани объекта которые обращены по направлению от камеры.

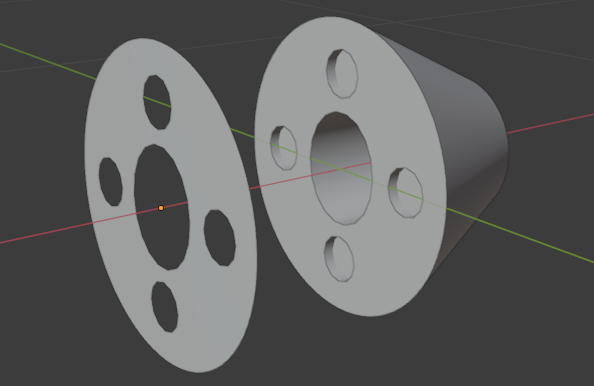
Изображение 4 – Бэкфейсы космического корабля

Вычисления будем проводить в три этапа. Каждый этап – это один проход или pass в шейдере. В рамках одного прохода вычисления выполняются параллельно, а его результаты могут быть использованы в последующих проходах.

Для начала нам нужно поставить камеру с ортографической проекцией, которая не искажает размер объектов в зависимости от расстояния до них. Далее мы будем снимать объекты этой камерой и обрабатывать полученные данные в шейдере.

На первом этапе найдем расстояние от камеры до стыковочной части корабля для каждого пикселя на текстуре.

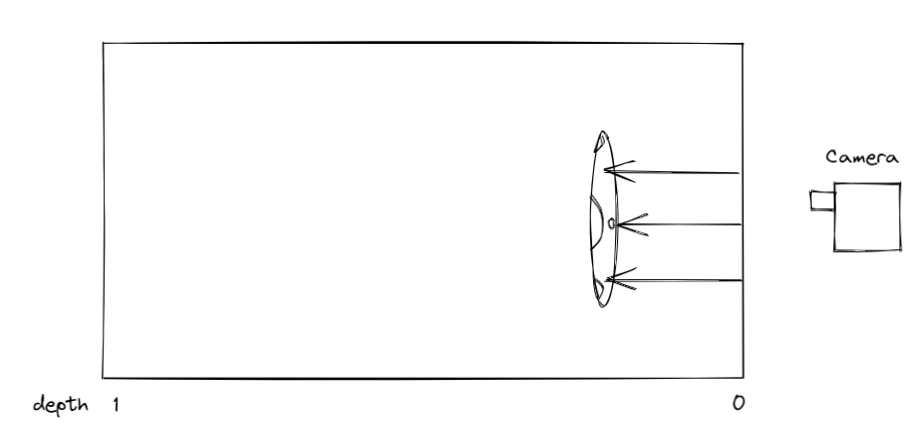
Изображение 5 – Демонстрация нахождения расстояния до стыковочной части корабля

Изображение 6 – Результат первого этапа

В каждом пикселе на текстуре хранится значение расстояния – глубина объекта.

На втором этапе найдем расстояние от камеры до бэкфейсов астероида.

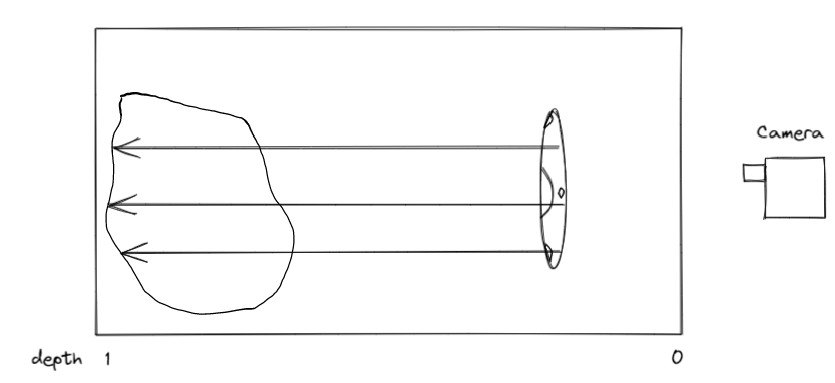
Изображение 7 – Демонстрация нахождения расстояния до бэкфейсов астероида

В один пиксель может попадать несколько бэкфейсов. Нас интересуют минимальные расстояния между кораблем и астероидом. Поэтому мы будем рассматривать расстояние до всех задних граней станции, но в текстуру записывать только одно – минимальное.

А затем сопоставим пиксели с текстурой из первого этапа и возьмем значение цвета для каждого пикселя. Это будет являться расстоянием от камеры до корабля. Теперь просто вычтем его из расстояния до станции и получим расстояние между кораблем и космической станцией. Запишем полученное расстояние как значение пикселя в новой текстуре.

Изображение 8 – Результат второго этапа

На третьем этапе найдем расстояние от камеры до фронтфейсов астероида – передних граней объекта которые обращены по направлению к камере. Сделаем это для каждого пикселя на текстуре.

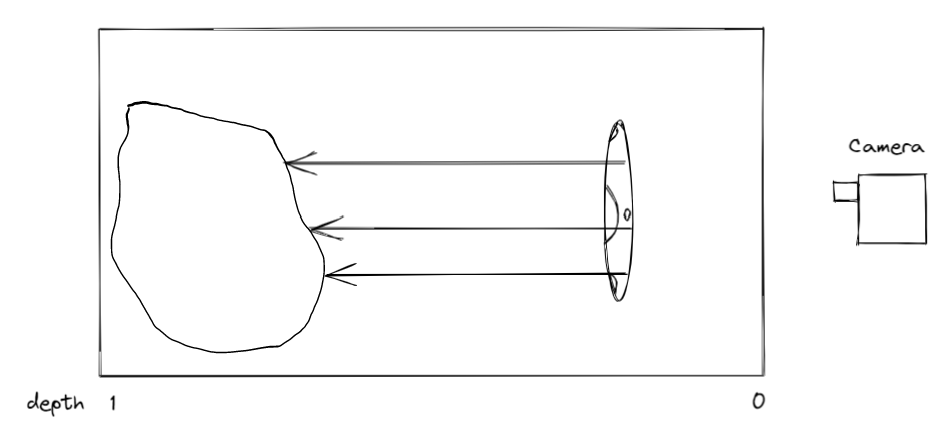
Изображение 9 – Демонстрация нахождения расстояния до фронтфейсов астероида

А затем, также как во втором этапе, сопоставим пиксели с текстурой из первого этапа и найдем расстояние между кораблем и передними гранями астероида.

Полученные значения запишем в текстуру с предыдущего этапа. В итоге мы получаем текстуру – изображение, в котором закодированы наименьшие расстояния от стыковочной части корабля до астероида.

Изображение 10 – Результат третьего этапа

При вычитании глубин мы можем получить отрицательные значения, поэтому нужно использовать дополнительную логику, для того чтобы возвращать значения в правильном формате.

Далее мы получаем текстуру в коде, проходимся в цикле по каждому пикселю, получаем значения цвета, распаковываем их и обрабатываем. Сложность этого алгоритма O(n²), где n – это размер текстуры. Для решения задачи нам было достаточно текстуры размером 128х128 пикселей. При этом шейдер позволяет нам автоматически подстраивать этот размер под девайс, на котором он работает.

Если полученное значение для пикселя отрицательное, это значит, что стыковочная часть корабля пересекает поверхность астероида – вершины первого объекта находятся внутри второго.

Для вывода результата на экран создадим текстуру и покрасим в оранжевый те пиксели где расстояние отрицательное. Остальные пиксели корабля покрасим в зеленый.

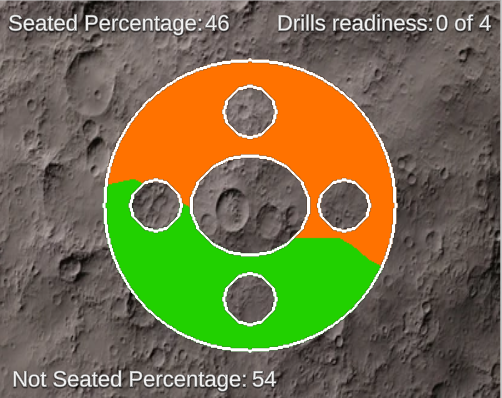
Изображение 11 – Результат четвёртого этапа

Посадка стержней

В предыдущей главе мы построили карту пересечения нижней части корабля и астероида. Но для завершения посадки нам необходимо закрепить космический корабль на астероиде с помощью стержней-буров. Все четыре стержня должны находиться внутри астероида. Эта задача отличается от первой тем, что нам необходимо найти пересечение объёмов. Соответственно, мы не можем отрезать лишние части, как в первом случае. Однако мы можем упростить нашу модель и разрезать её на некоторое количество плоскостей с определенным шагом.

Изображение 12 – Упрощение модели бура

Изображение 13 – Разделение бура на множество плоскостей

Идея алгоритма состоит в том, чтобы представить эти плоскости в бинарном виде. Так как шейдер возвращает четырехкомпонентый вектор, где каждый компонент содержит 32 бита, у нас есть 128 слотов, в которые мы можем записать какую-либо информацию. Таким образом, мы можем разместить каждую плоскость в определенный слот, основываясь на значении ее глубины – расстоянии от камеры до плоскости.

Из-за особенностей бинарного представления типа float, мы не можем использовать часть слотов. Так как первый бит зарезервирован под знак, и следующие восемь под экспоненту, у нас есть всего 92 свободных слота. И если плоскостей больше, нам необходимо обрабатывать их в несколько подходов, записывая результат в разные текстуры.

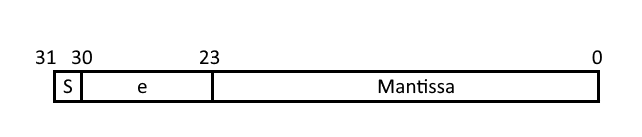
Изображение 14 – Представление типа данных float в памяти

Очень важно правильно поставить камеру перед началом вычислений: она должна находиться у основания стержня и быть ортографической.

Итак, на первом этапе мы находим расстояние от камеры до каждой плоскости. А затем на основе этого значения определяем, в какой из свободных слотов нам нужно поместить эту плоскость. Для этого мы предполагаем что в 92 слотах должны находиться значения от 0 до 1, где 0 находится в слоте 32, и 1 в слоте 105 и делаем несложные математические вычисления.

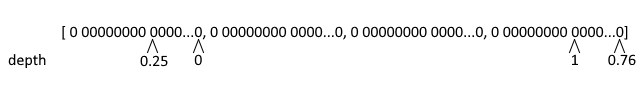
Изображение 15 – Сопоставление глубины объекта и позиции слота

Мы повторяем эти действия для каждого пикселя на текстуре. Также необходимо настроить смешивание, так как у нас есть множество точек, которые попадают в один и тот же пиксель. Здесь мы должны учитывать каждую плоскость для правильных расчетов, поэтому будем складывать значения, и записывать сумму всех глубин, которые попадают в этот пиксель.

Мы заранее нарезали плоскости таким образом, чтобы каждая из плоскостей попадала в свой определенный слот, а значит при сложении результатов у нас не будет проблем с тем, что значения в слотах будут пересекаться. Пример сложения глубин представлен на картинке ниже:

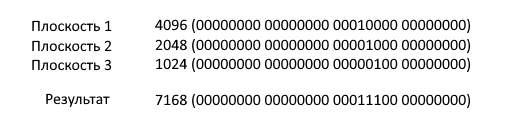
Изображение 16 – Результат сложения глубин в разных плоскостях

На втором этапе мы делаем те же самые действия, но уже для граней астероида. После того, как мы определили, в каком из слотов находятся эти грани для каждого пикселя, мы находим значение для того же самого пикселя на текстуре из первого этапа и делаем побитовое сравнение. Простыми словами, мы сравниваем нули и единицы, и если единица находится в одном и том же слоте для обоих чисел, это значит, что глубина одной из плоскостей стержня и астероида одинаковы, и, следовательно, они пересекаются.

Изображение 17 – Сравнение глубины плоскостей стержня-бура и астероида

После второго этапа мы возвращаем текстуру, в каждом пикселе которой записан результат пересечения двух объектов. Мы получаем и обрабатываем эту текстуру в коде на CPU – проходимся по всем пикселям и находим какие из стержней находятся вне астероида.
Раскрасим пиксели таких стержней в оранжевый цвет на нашей конечной текстуре, а пиксели остальных стержней – в зелёный.

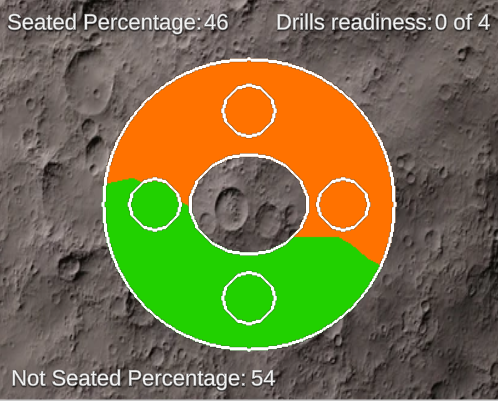
Изображение 18 – Финальная текстура, содержащая информацию о пересечении объектов

Видео 1 – Визуализация работы алгоритма в зависимости от положения корабля относительно астероида

Итак, мы, наконец, отображаем все необходимые данные на экране.

Плюсы и минусы алгоритма

Очевидно, что этот способ более производительный. Мы буквально на лету пересчитываем карту пересечения двух объектов, и не загружаем ресурсы CPU, что позволяет выполнять другую тяжелую логику одновременно с расчетами.

Однако вычисление значений на GPU имеет свои минусы.

Главный из них – это то, что точность вычислений зависит от конкретной видеокарты. На практике нам пришлось искусственно понижать точность, для того чтобы результаты были одинаковыми на всех устройствах.

Второй минус – это поддержка текстур. Если алгоритм необходимо запускать на нескольких платформах, как в нашем случае – на WebGL и iOS, придется подбирать такую текстуру которая поддерживается на всех платформах. Изначально мы планировали использовать формат текстуры RGBA float – где каждый из четырех компонентов содержит 32 бита информации, однако из-за кроссплатформенных ограничений нам пришлось использовать формат RG float – всего два компонента, каждый из которых содержит 32 бита информации. Это усложнило код шейдеров и увеличило количество этапов вычислений.

Еще одним недостатком является необходимость в предварительной подготовке и упрощении модели для выполнения расчётов.